Topological Sort

The topological sort is a little different from other sorting algorithms.

a topological sortortopological orderingof a directed graph is a linear ordering of its vertices such that for every directed edge/uv/from vertex/u/to vertex/v/,/u/comes before/v/in the ordering

For example, if we have a directed acyclic graph (DAG), a vertex before the edge is always smaller than the current vertex.

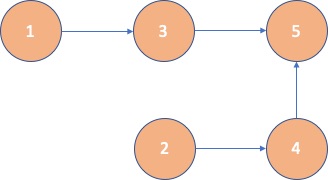
This is a valid topological ordering because the current vertex is always greater than previous vertices.

How about the below graph?

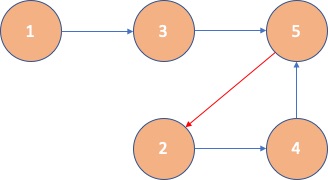
This is not a topological ordering, because 2 is smaller than 5 and has the edge from 5 to 2.

Importantly, we can also see the cycle 2 -> 4 -> 5 -> 2. if a graph has a cycle, we cannot have a valid topological ordering.

Algorithm

Let’s say that DAG is represented as adjaceny list

graph = [ [], [], [], [ 1 ], [ 2 ], [ 3, 4 ], [] ] (index 5 represents node 5 and graph[5] represents its edges that come from other nodes, which is 3 and 4.)

From the graph, we know that the topological order should be 1, 3, 2, 4, 5 or 2, 4, 1, 3, 5. But how do we implement this in code?

An algorithm for topological sorting is based on depth-first search . We can start with the smallest number and explore its neighbors in a dearth-first manner, and as visit a node we mark the node as visited in order to prevent revisit the node in the future.

Once we hit the node that cannot visit other nodes anymore, we mark the node with an order number and backtrack to the previous node.

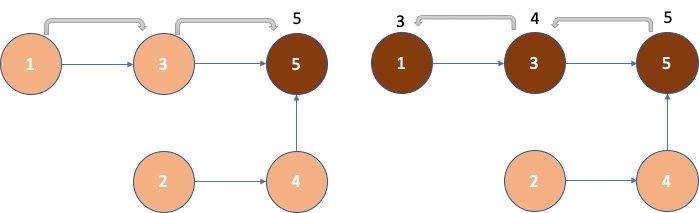
It doesn’t matter whether we choose 2 or 4 after mark 1 as visited.

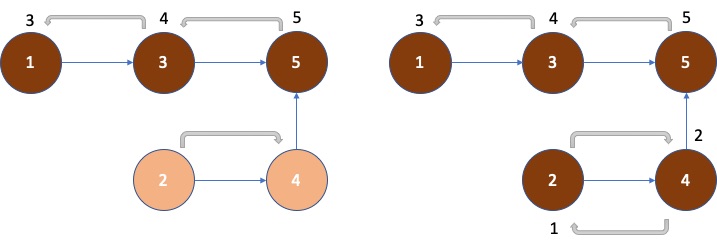
In this example, we got 2, 4, 1, 3, 5, but if we start from node 2, we will get different valid topological order.

A topological sort is useful for ordering the tasks or the schedule that has a dependency.

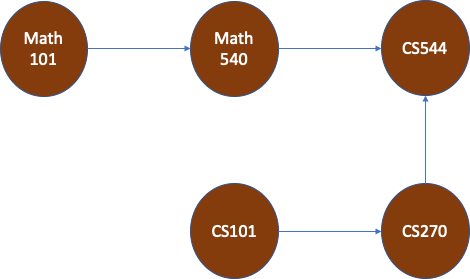
For example, if we have five courses to take and want to know which course should take first, topological sorting is a good approach to solve. Answer is CS101 -> CS270 -> Math101 -> Math540 -> CS544

Exercise

I found a problem that can be solved with a topological sort algorithm. Can you solve the question by using a topological sort algorithm?

Course Schedule - LeetCode